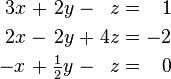คณิตศาสตร์

วันพฤหัสบดีที่ 5 กุมภาพันธ์ พ.ศ. 2558

ระบบสมการเชิงเส้น

ระบบสมการเชิงเส้น เป็นหมู่สมการเชิงเส้นที่เกี่ยวข้องกับตัวแปรชุดเดียวกัน ตัวอย่างเช่น

\begin{alignat}{7} 3x &&\; + \;&& 2y &&\; - \;&& z &&\; = \;&& 1 & \\ 2x &&\; - \;&& 2y &&\; + \;&& 4z &&\; = \;&& -2 & \\ -x &&\; + \;&& \tfrac{1}{2} y &&\; - \;&& z &&\; = \;&& 0 & \end{alignat}

เป็นระบบสามสมการที่มีสามตัวแปร

x, y, z

ผลเฉลยของระบบสมการเชิงเส้นเป็นการแทนค่าจำนวนในตัวแปรซึ่งทำให้สมการทั้งหมดสอดคล้องกันพร้อมกัน ผลเฉลยของระบบสมการเชิงเส้นข้างต้น คือ

\begin{alignat}{2} x &\,=\,& 1 \\ y &\,=\,& -2 \\ z &\,=\,& -2 \end{alignat}

เพราะทำให้ทั้งสามสมการสมเหตุสมผล คำว่า "ระบบ" เป็นการชี้ว่าต้องพิจารณาสมการทั้งหมดร่วมกัน ไม่ใช่แยกกัน

ในวิชาคณิตศาสตร์ ทฤษฎีระบบสมการเชิงเส้นเป็นพื้นฐานและส่วนหลักมูลของพีชคณิตเชิงเส้น หัวข้อซึ่งใช้ในคณิตศาสตร์สมัยใหม่ส่วนมาก ขั้นตอนวิธีการคณนาสำหรับการหาผลเฉลยเป็นส่วนสำคัญของพีชคณิตเชิงเส้นตัวเลข และมีบทบาทเด่นในวิชาวิศวกรรมศาสตร์ ฟิสิกส์ เคมี วิทยาการคอมพิวเตอร์และเศรษฐศาสตรฺ ระบบสมการไม่เชิงเส้นมักประมาณโดยใช้ระบบสมการเชิงเส้นได้ ซึ่งเป็นเทคนิคที่ช่วยได้มากเมื่อสร้างแบบจำลองทางคณิตศาสตร์หรือการจำลองระบบที่ค่อนข้างซับซ้อนทางคอมพิวเตอร์ อ่านเพิ่มเติมhttp://th.wikipedia.org/wiki/%E0%B8%A3%E0%B8%B0%E0%B8%9A%E0%B8%9A%E0%B8%AA%E0%B8%A1%E0%B8%81%E0%B8%B2%E0%B8%A3%E0%B9%80%E0%B8%8A%E0%B8%B4%E0%B8%87%E0%B9%80%E0%B8%AA%E0%B9%89%E0%B8%99

ฟังก์ชันสัมบูรณ์

ค่าสัมบูรณ์ หรือ มอดุลัส (อังกฤษ: absolute value หรือ modulus) ในคณิตศาสตร์ คือ ผลต่างระหว่างจำนวนนั้นกับ 0 พูดง่ายๆคือ จำนวนที่ไม่มีเครื่องหมายลบ ตัวอย่างเช่น 3 คือค่าสัมบูรณ์ของ 3 และ −3 นิยามได้ดังนี้: สำหรับจำนวนจริงใดๆ a, ค่าสัมบูรณ์ของ a เขียนแทนด้วย |a| เท่ากับ a ถ้า a ≥ 0 และเท่ากับ −a ถ้า a < 0 (ดูเพิ่มเติม: อสมการ) |a| จะไม่เป็นจำนวนลบ ค่าสัมบูรณ์จะเป็นจำนวนบวกหรือศูนย์เสมอ นั่นคือจะไม่มีค่า a ที่ |a| < 0
ค่าสัมบูรณ์สามารถถือว่าเป็นระยะทางของจำนวนนั้นจากศูนย์ สัญกรณ์ของระยะทางในคณิตศาสตร์มักเขียนในรูปค่าสัมบูรณ์อยู่เสมอ เมื่อจำนวนจริงถูกพิจารณาเหมือนเป็นเวกเตอร์หนึ่งมิติ ค่าสัมบูรณ์คือขนาด และ p-นอร์มสำหรับ p ใดๆ ที่ตัวประกอบคงที่ ทุกๆนอร์มใน R¹ จะเท่ากับค่าสัมบูรณ์: ||x||=||1||.|x| อ่านเพิ่มเติมhttp://th.wikipedia.org/wiki/%E0%B8%84%E0%B9%88%E0%B8%B2%E0%B8%AA%E0%B8%B1%E0%B8%A1%E0%B8%9A%E0%B8%B9%E0%B8%A3%E0%B8%93%E0%B9%8C

วันพฤหัสบดีที่ 29 มกราคม พ.ศ. 2558

ฟังก์ชัน

ฟังก์ชัน คือ ความสัมพันธ์ จาก เซต หนึ่ง (โดเมน) ไปยังอีกเซตหนึ่ง (โคโดเมน ไม่ใช่ เรนจ์) โดยที่สมาชิกตัวหน้าไม่ซ้ำกัน ความคิดรวบยอดของฟังก์ชันนี้เป็นพื้นฐานของทุกสาขาของคณิตศาสตร์และวิทยาศาสตร์เชิงปริมาอ่านเพิ่มเติมhttp://th.wikipedia.org/wiki/%E0%B8%9F%E0%B8%B1%E0%B8%87%E0%B8%81%E0%B9%8C%E0%B8%8A%E0%B8%B1%E0%B8%99_(%E0%B8%84%E0%B8%93%E0%B8%B4%E0%B8%95%E0%B8%A8%E0%B8%B2%E0%B8%AA%E0%B8%95%E0%B8%A3%E0%B9%8C)